

 Visão geral do jogo
Visão geral do jogo
ENJOY THE BEAUTY AND ENIGMA OF TOPOLOGY !!!
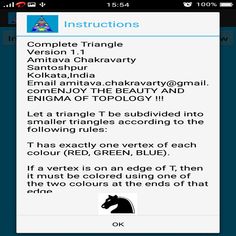
Let a triangle T be subdivided into smaller triangles according to the following rules:
T has exactly one vertex of each colour (RED, GREEN, BLUE).
If a vertex is on an edge of T, then it must be colored using one of the two colours at the ends of that edge.
The vertices inside T can be colored by any color RED, GREEN OR BLUE.
Then there is a small sub triangle (actually odd number of sub triangles) in the subdivision process that has exactly one vertex of each color.
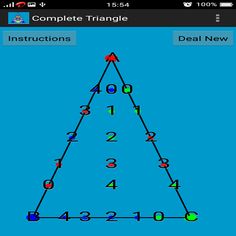
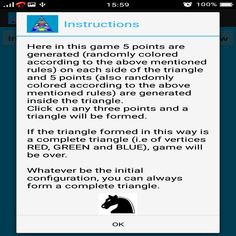
Here in this game 5 points are generated (randomly colored according to the above mentioned rules) on each side of the triangle and 5 points (also randomly colored according to the above mentioned rules) are generated inside the triangle.
Click on any three points and a white triangle will be formed.
Clicked points are joined by a white line.
If the triangle formed in this way is a complete triangle (i.e of vertices RED, GREEN and BLUE), game will be over.
Whatever be the initial configuration, you can always form a complete triangle.
BUG :
If you click on the vertices of the boundary triangle, the game will also be over.
Proper triangulation is not checked.
Display may be distorted in smaller screen.
This game is ABSOLUTELY FREE, has NO-ADS or IN-APP PURCHASES.
In case of any bug or misinformation, please email me.
T has exactly one vertex of each colour (RED, GREEN, BLUE).
If a vertex is on an edge of T, then it must be colored using one of the two colours at the ends of that edge.
The vertices inside T can be colored by any color RED, GREEN OR BLUE.
Then there is a small sub triangle (actually odd number of sub triangles) in the subdivision process that has exactly one vertex of each color.
Here in this game 5 points are generated (randomly colored according to the above mentioned rules) on each side of the triangle and 5 points (also randomly colored according to the above mentioned rules) are generated inside the triangle.
Click on any three points and a white triangle will be formed.
Clicked points are joined by a white line.
If the triangle formed in this way is a complete triangle (i.e of vertices RED, GREEN and BLUE), game will be over.
Whatever be the initial configuration, you can always form a complete triangle.
BUG :
If you click on the vertices of the boundary triangle, the game will also be over.
Proper triangulation is not checked.
Display may be distorted in smaller screen.
This game is ABSOLUTELY FREE, has NO-ADS or IN-APP PURCHASES.
In case of any bug or misinformation, please email me.
Desenvolvedor
AMITAVA CHAKRAVARTY (AC)Data de atualização
Mar 13, 2018Data de lançamento
Mar 02, 2018Preço
Grátis Desenvolvedor
Desenvolvedor
Mais jogos de AMITAVA CHAKRAVARTY (AC)